One day I decided to challenge myself by trying to implement multithreaded quicksort. I wanted to see how it would compare to the built-in Array.Sort() method.
I came up with two algorithms that were 2-4x faster than Array.Sort():
- Top-down: divide-fork-sort-merge
- Bottom-up: quicksort with fork-on-recursion
After continuing to tinker, in attempts to further optimize, I came across the AsParallel().OrderBy() method (PLINQ). After reading about this, I realized it was the same approach as my divide-fork-sort-merge algorithm. I did a performance test and it was also 2-4x faster than Array.Sort().
In the end, I’d use the built-in AsParallel().OrderBy() method in production software if the input were relatively large. Otherwise I’d stick to the regular built-in methods for sorting a list/array. In general it’s a good idea to use built-in functionality instead of rolling your own, because it keeps your code clean and simple.
Table of Contents
Primer on quicksort and why I wanted to make it threaded
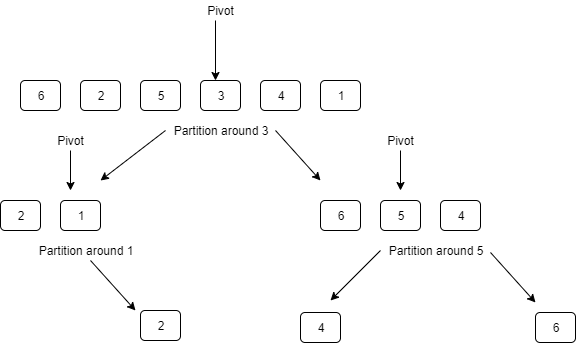
What is quicksort?
It’s a divide-and-conquer sorting algorithm that works like this:
Pick a pivot
Partition the array around the pivot
left subarray = any element <= pivot
right subarray = any element > pivot
Quicksort(left subarray)
Quicksort(right subarray)Code language: plaintext (plaintext)Here’s what this looks like:
Why divide-and-conquer algorithms, like quicksort, benefit from multithreading
Multiple threads help speed things up if:
- The processor has multiple cores, and therefore can run multiple threads concurrently.
- The work can be divided into non-overlapping partitions
Because quicksort divides the array into two non-overlapping subarrays at each step, it meets the second condition, and the work can be parallelized.
Comparing performance
To compare performance I generated an array with random elements, then copied this array into other arrays for each algorithm I was testing. This was to make sure the algorithms were sorting the exact same sequence of elements. Then I used System.Diagnostics.Stopwatch to measure the elapsed time of each algorithm.
var approach1Array = SortUtility.GenRandomArray<string>(size: 10_000_000);
Console.WriteLine("Size " + approach1Array.Length);
var approach2Array = new string[approach1Array.Length];
Array.Copy(approach1Array, approach2Array, approach2Array.Length);
Stopwatch approach1Stopwatch = new Stopwatch();
approach1Stopwatch.Start();
Array.Sort(approach1Array);
approach1Stopwatch.Stop();
Console.WriteLine($"Array.Sort - Is sorted? {SortUtility.IsSorted(approach1Array)}. ElapsedMS={approach1Stopwatch.ElapsedMilliseconds}");
Stopwatch approach2Stopwatch = new Stopwatch();
approach2Stopwatch.Start();
approach2Array = approach2Array.AsParallel().OrderBy(t => t).ToArray();
approach2Stopwatch.Stop();
Console.WriteLine($"PLINQ.Sort - Is sorted? {SortUtility.IsSorted(approach2Array)}. ElapsedMS={approach2Stopwatch.ElapsedMilliseconds}");
Code language: C# (cs)Here are the utility functions I used for generating input and verifying sorted order.
public static T[] GenRandomArray<T>(int size = 10000)
{
var a = new T[size];
Random r = new Random();
for (int i = 0; i < size; i++)
{
a[i] = (T)Convert.ChangeType(r.Next(Int32.MinValue, Int32.MaxValue), typeof(T));
}
return a;
}
public static bool IsSorted<T>(T[] a) where T : IComparable<T>
{
if (!a.Any())
return true;
var prev = a.First();
for (int i = 1; i < a.Length; i++)
{
if (a[i].CompareTo(prev) < 0)
return false;
prev = a[i];
}
return true;
}
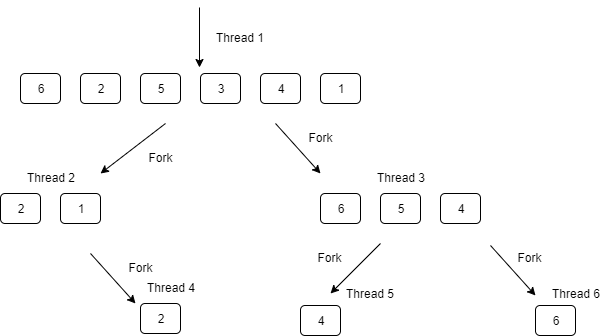
Code language: C# (cs)Bottom-up: quicksort with fork-on-recursion
I made a modification to the quicksort algorithm. After partitioning, it’s quicksorting the left and the right subarrays in their own threads concurrently.
Pick a pivot
Partition the array around the pivot
left subarray = any element <= pivot
right subarray = any element > pivot
Fork Quicksort(left subarray)
Fork Quicksort(right subarray)Code language: plaintext (plaintext)Diagram
To illustrate this, every time the call tree branches, it is also forking the work.
Code
public class ThreadedQuickSort<T> where T : IComparable<T>
{
public async Task QuickSort(T[] arr)
{
await QuickSort(arr, 0, arr.Length - 1);
}
private async Task QuickSort(T[] arr, int left, int right)
{
if (right <= left) return;
int lt = left;
int gt = right;
var pivot = arr[left];
int i = left + 1;
while (i <= gt)
{
int cmp = arr[i].CompareTo(pivot);
if (cmp < 0)
Swap(arr, lt++, i++);
else if (cmp > 0)
Swap(arr, i, gt--);
else
i++;
}
var t1 = Task.Run(() => QuickSort(arr, left, lt - 1));
var t2 = Task.Run(() => QuickSort(arr, gt + 1, right));
await Task.WhenAll(t1, t2).ConfigureAwait(false);
}
private void Swap(T[] a, int i, int j)
{
var swap = a[i];
a[i] = a[j];
a[j] = swap;
}
}
Code language: C# (cs)Performance
Size 10000000
Array.Sort - Is sorted? True. ElapsedMS=45740
Bottomup-Quicksort-ForkOnRecursion (mine) - Is sorted? True. Elapsed=19801
PLINQ.Sort - Is sorted? True. ElapsedMS=15551Code language: plaintext (plaintext)What doesn’t work
The key problem is the top-level thread needs to know when all child threads have completed. The simplest way I found to do this was by using await/async and Tasks.
I attempted to spawn new threads, and then calling Thread.Join(). With a large enough input, this quickly resulted in OutOfMemoryExceptions.
I tried to use ThreadPool threads. As mentioned above, the top-level thread needs to know about the child threads and when they have completed. This can’t be done with recursion, because there’s a race condition. It can be done using iterative quicksort – using CountdownEvent to signal the top-level waiter – but with this approach you have to partition all the way down to a predetermined limit (let’s say 1024 elements), and then sort those in a new thread. This defeats the purpose of multithreading. The gains in performance come from dividing the work into multiple threads right away.
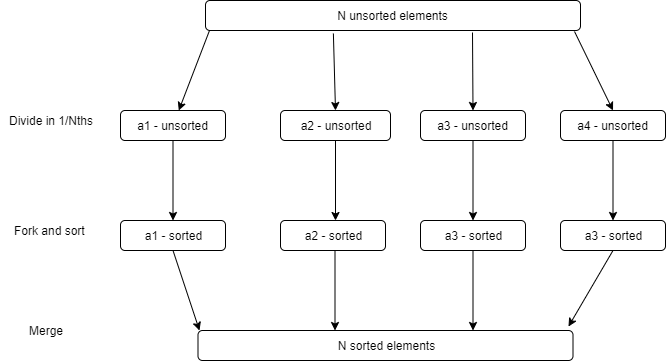
Top-down: divide-fork-sort-merge
I randomly thought of this algorithm, wrote it down, then implemented it. Later on I found out that this is approach is the Fork-Join pattern.
Divide array into 4 subarrays
For each subarray
Fork Sort(subarray)
4-way merge subarraysCode language: plaintext (plaintext)Diagram
Code
public class ForkJoinSort<T> where T : IComparable<T>
{
public async Task Sort(T[] a)
{
var arrs = Divide(a);
List<Task> tasks = new List<Task>();
foreach (var arr in arrs)
{
var tmp = arr;
tasks.Add(Task.Run(() => { Array.Sort(tmp); }));
}
await Task.WhenAll(tasks.ToArray()).ConfigureAwait(false);
Merge(a, new List<Arr>
{
new Arr() { a = arrs[0], ptr = 0 },
new Arr() { a = arrs[1], ptr = 0 },
new Arr() { a = arrs[2], ptr = 0 },
new Arr() { a = arrs[3], ptr = 0 },
});
}
private class Arr
{
public T[] a;
public int ptr;
}
private static void Merge(T[] destArr, List<Arr> arrs)
{
T minValue;
Arr min;
for (int i = 0; i < destArr.Length; i++)
{
var firstArr = arrs.First();
minValue = firstArr.a[firstArr.ptr];
min = firstArr;
for (int j = 1; j < arrs.Count; j++)
{
if (arrs[j].a[arrs[j].ptr].CompareTo(minValue) < 0)
{
minValue = arrs[j].a[arrs[j].ptr];
min = arrs[j];
}
}
destArr[i] = minValue;
min.ptr++;
if (min.ptr >= min.a.Length)
{
arrs.Remove(min);
}
}
}
private List<T[]> Divide(T[] a)
{
List<T[]> arrs = new List<T[]>();
int divisionSize = a.Length / 4;
var a1 = new T[divisionSize];
var a2 = new T[divisionSize];
var a3 = new T[divisionSize];
var a4 = new T[a.Length - (divisionSize * 3)];
Array.Copy(a, 0, a1, 0, a1.Length);
Array.Copy(a, divisionSize, a2, 0, a2.Length);
Array.Copy(a, divisionSize * 2, a3, 0, a3.Length);
Array.Copy(a, divisionSize * 3, a4, 0, a4.Length);
return new List<T[]>()
{
a1, a3, a2, a4
};
}
}
Code language: C# (cs)Performance
Size 10000000
Array.Sort - Is sorted? True. ElapsedMS=44544
PLINQ.Sort - Is sorted? True. ElapsedMS=15213
Topdown-ForkJoinSort - Is sorted? True. Elapsed=18240Code language: plaintext (plaintext)What doesn’t work
Divide takes a trivial amount of time, Sort takes 80%, and Merge takes 20% of the time.
It may seem odd that the array is divided into 4 equal parts. The main temptation is to try to partition the array, such that a1 < a2 < a3 < a4, which then makes the merging step trivial. The primary problem is picking a good pivot is hard. The same is true for quicksort itself. Why? Because, in order to pick the best pivot, you really need the middle-most element, which would require n^2 comparisons (in other words, you have to sort first in order to pick a good partition).
By random chance, you’ll sometimes end up with the left partition having 95% of the elements, thereby making the multithreading pointless. By random chance, you’ll also end up with the perfect partition sometimes. Therefore, it makes more sense to just evenly partition the arrays.
The other main optimization temptation is to detect “streaks” while merging, and then bulk-copying to the target array. However, this suffers from the same problem as what was mentioned above. In the worst case, the mins will never be pulled from the same array twice in a row. In most cases, the streaks will be small, and not worth the overhead of trying to keep track of “streaks.”
It’s interesting that simplicity is the best approach here due to randomness making “smarter” approaches ineffective.
PLINQ.AsParallel().OrderBy()
The AsParallel().OrderBy() built-in method (PLINQ) uses the Fork-Join algorithm. Here’s how to use it sort an array:
arr = arr.AsParallel().OrderBy(t => t).ToArray();
Code language: C# (cs)That’s it. Simple.
There are two reasons why I would always choose this over my homemade algorithms:
- It abstract away complexity, making my code very simple
- It usually outperforms my algorithms by a little bit.
Comments are closed.